How to converting fractions to decimals and and vice versa
Fractions to decimals, decimals to fractions. Many numbers can be written as both. But how do you know which is which, when to use what and how to convert between the two? Read on to find out. It’s not as tricky as it might seem.

Super Simple Conversions
The simplest conversions are those where the fractions and decimals sound exactly alike when read aloud. Not sure what we mean? Let’s look at a few examples.
$$\frac{48}{100}$$ is read as forty-eight hundredths
0.48 is also read as forty-eight hundredths
You guessed it, they’re equivalent!
$$\frac{48}{100} = 0.48$$

It works in reverse too. Consider this problem.
Write 0.432 as a fraction.
First, read the decimal aloud – zero and four hundred thirty-two thousandths. Turn it into a fraction? What then? It goes back to elementary school again. I hope.
Now, write that as a fraction $$\frac{432}{1000}$$.
(Thousandths tells you that the denominator will be 1000 and four hundred thirty-two tells you that the numerator will be 423.)
Let’s try another example.
Write $$\frac{58}{100}$$ as a decimal.
First, read the fraction aloud – Fifty-eight hundredths.
Now, write that as a decimal 0.58.
These simple conversions are as easy as correctly reading the fractions and decimals aloud. No extra work required. I hope you listened to your elementary teachers!!
Fractions to Decimals
Unfortunately, not all conversions are quite so easy. The “read it aloud” method only works for 10s, 100s, 1000s, and so on. The following methods, however, work for every decimal/fraction conversion problem ever written so read on, learn how and you’ll be set on these conversions for life.
Let’s start with converting fractions to decimals. Simply think of the fraction bar as a division sign and rewrite the fraction as a division problem.
or example:$$\frac{5}{8}$$= 5 divided by 8.

Now, you can do one of two things: either enter the problem in your calculator (the easy way out!) OR think back to 4th grade and do some long division!
Either way, you’ll find that 5 divided by 8 = 0.625
That’s it, you’re done! $$\frac{5}{8}$$= 0.625
Let’s try another problem.
How about $$\frac{24}{30}$$? Write $$\frac{24}{30}$$ as a decimal.
Alright, remember you need to think of the fraction bar as a division sign and re-write the fraction as a division problem.
$$\frac{24}{30}$$= 24 divided by 30.
Again, enter it into your calculator or put your long division skills to work. The division will leave you with an answer of 0.8.
Now you know that $$\frac{24}{30}$$= 0.8.
**You might also notice that 24/30=8/10 when reduced (divide both numerator and denominator by 3). So 8/10=0.8 which takes us back to the “read it out loud” method of converting we discussed earlier.
What if it doesn’t work out?
Sometimes you do the division and things work out to a nice simple decimal like 0.8. Sometimes, that’s not the case. Enter the repeating decimal.
Let’s say you go to divide and you end up with a remainder…what then!? Read on to find out.
Let’s use $$\frac{1}{3}$$ for our example. We know that the fraction bar is really a division sign so we can re-write the problem like this: 1 divided by 3 = ?
Now, we go to solve and 3 can’t divide into one so we have to insert a decimal and some zeros to help us out. Take a look at the problem below.
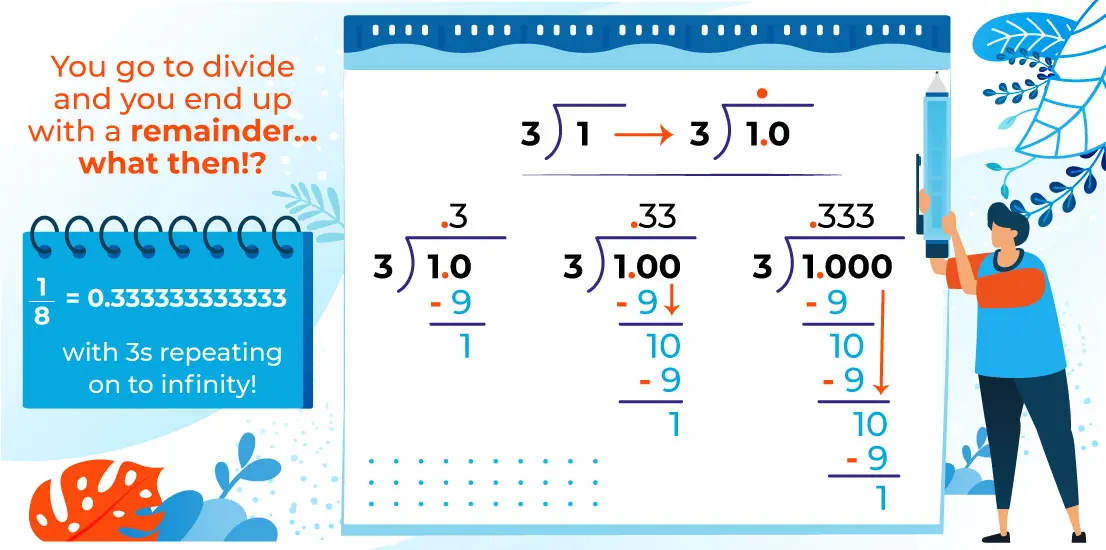
One can easily be re-written as the decimal 1.0. Then you’ll ask yourself…”how many times does 3 fit into 10?” You’ll add a three in the quotient to the right of the decimal, multiply to get 9 and subtract to get one. Then it’s time to add another zero and bring it down. Once again you’ll find yourself asking the question…”how many times does 3 fit into 10?” Spoiler alert! This pattern will repeat itself over and over and over again!! That’s how we know that 1/3 is actually a repeating decimal.$$\frac{1}{3}$$ = 0.333333333333 with 3s repeating on to infinity!
Converting the Opposite Direction – Decimals to Fractions
Now that you know how to handle conversions of fractions to decimals (even when they don’t work out super easily!) let’s consider those problems where you’re asked to convert in the opposite direction. What if you’re given a decimal and you need to turn it into a fraction? What then? It goes back to elementary school again. I hope you listened to your teacher when she taught you how to properly read decimals aloud!
Let’s take a look at some examples.
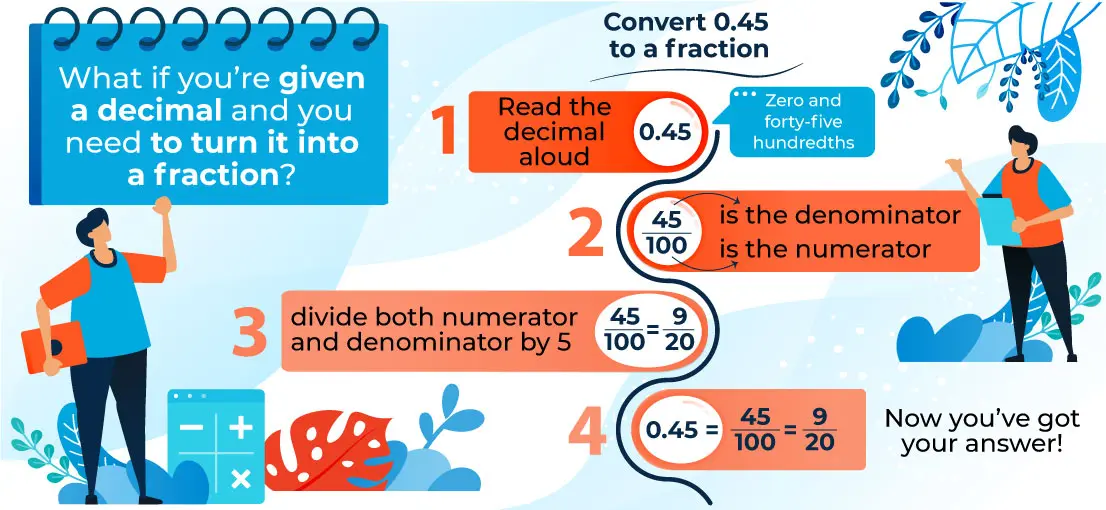
Convert 0.45 to a fraction.
- First, read the decimal aloud. Zero and forty-five hundredths.
- You just read yourself the fraction too!$$\frac{45}{100}$$ the hundredths is the denominator and the forty-five is the numerator.
- Now $$\frac{45}{100}$$ is not in lowest terms so you can reduce from here.
- First divide both numerator and denominator by 5. $$\frac{45}{100}$$ =$$\frac{9}{20}$$
- Now you’ve got your answer! 0.45 =$$\frac{45}{100}$$=$$\frac{9}{20}$$
Let’s try one more:
Write 0.876 as a fraction.
- Remember, start by reading it aloud – zero and eight-hundred seventy-six thousandths.
- Thousandths tells you your denominator is 1000 and eight-hundred seventy-six tells you your numerator is 876 so…
- Your answer is $$\frac{876}{1000}$$. Now you’ll likely want to reduce!
- First, you can divide both numerator and denominator by two.
- $$\frac{876}{1000}$$=$$\frac{438}{500}$$
- Now you can divide by two again.
- $$\frac{438}{500}$$=$$\frac{219}{250}$$
- You’ve got your answer: 0.876 =$$\frac{219}{250}$$.
Converting fractions to decimals and back again may seem intimidating but it’s really not that hard! With a few simple things to remember you can handle it.